Inšpirácia pre učiteľov matematiky a prírodopisu
Parita patrí medzi jednoduchšie matematické pojmy. Má však významnú propedeutickú hodnotu, lebo je jedným z prvých abstraktných pojmov. Ďakujeme jej za úvahy, ktoré viedli k vnímaniu nekonečna ako „reálneho“ objektu. Cez ňu pytagorejci pochopili, že úvahy o konkrétnych číslach sa dajú nahradiť úvahami o ich spoločných vlastnostiach. Takýmto príkladom je dôkaz toho, že výsledok súčtu dvoch nepárnych čísel je párny. Využíva manipuláciu s kamienkami. Tento postup časom viedol k objavu ešte zložitejších zákonitostí.
Počítajme ako pytagorejci
Nepárne číslo dokážeme zobraziť dvomi radmi kamienkov, z ktorých jeden obsahuje o kamienok viac. Čísla 9 a 13 môžu vyzerať takto:

Ak chceme dokázať, že ich súčet dá párne číslo, môžeme postupovať takto:
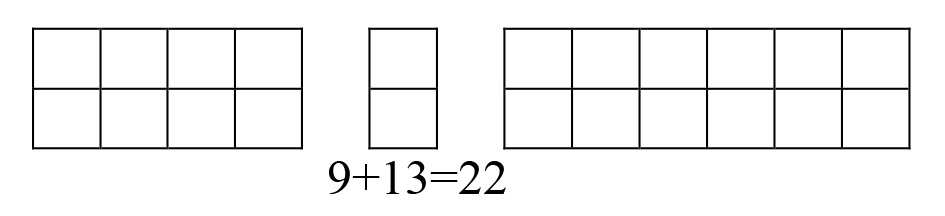
Vytŕčajúce kamienky spojíme do páru, čím vytvoríme súčet 8 + 2 + 12. Jeho výsledok musí byť zhodný so súčtom 9 + 13, lebo žiaden kamienok sme nepridali ani neubrali, len presunuli. Všetky sčítance sú teraz párne. Výsledok je tiež párny, ako vidieť z ich usporiadania. Navyše je zrejmé, že rovnako môžeme postupovať pri ľubovoľnej dvojici nepárnych čísel. Tvrdenie platí pre nekonečne veľa dvojíc.
Nekonečno nie je záhadou
Nekonečno teda nie je taký záhadný pojem, ako by sa mohlo zdať. Je to iba označenie pre neohraničené množstvo prípadov. (Matematika pozná aj iné nekonečná, tými však nebudeme čitateľa – ani žiakov – mýliť.)
Názorný dôkaz, ktorý použili pytagorejci, sa vyskytuje v mnohých úlohách. Tu sú dve z nich:
- Pre všetky celé čísla platí, že súčtom párneho a nepárneho čísla je nepárne číslo. Nakresli obrázok, pomocou ktorého to vysvetlíš.
- Zober postupnosť prirodzených čísel: 1, 2, 3, 4, 5, 6, 7, 8… Prečo je súčet každej dvojice po sebe idúcich čísel nepárny? (Počítaj 1+2, 2+3, 3+4… Určite ti niečo napadne.)
Parita je všade okolo nás
V ich riešení sa efektívne využíva parita. Tá hrá dôležitú úlohu nielen v matematike, ale aj v medziľudských vzťahoch: Na kvetoch margarét zvyknú zamilovaní počítať ľúbi-neľúbi. Spravidla začínajú slovom ľúbi. Od čoho závisí konečný výsledok? Kedy vyjde, že partner „ľúbi“ a kedy „neľúbi“?
Žiakov treba viesť k tomu, aby sa v ich odpovedi prejavila parita počtu okvetných lístkov. Diskusiu treba orientovať tak, aby rozvíjala poznatky z botaniky. Kým margaréty majú veľký a nepravidelný počet okvetných lístkov, pri iných rastlinách (s ich menším počtom) sa výsledok dá predpovedať. Tento cieľ sledujú otázky: Počet lupienkov margarét sa nedá vopred odhadnúť. Preto je výsledok počítania nepredvídateľný. S ktorými kvetmi by mal počítať ľúbi-neľúbi ten, kto chce, aby mu vždy vyšlo „ľúbi“? Ktorým slovom by mal začať?
Samozrejme, existuje aj rad zovšeobecnení matematických vyššie uvedených úloh. Napríklad:
- Aké pravidlá platia pre sčítanie troch celých čísel? Kedy bude výsledok párny a kedy nepárny?
- Ulož kamienky tak, aby vytvárali štvorce:
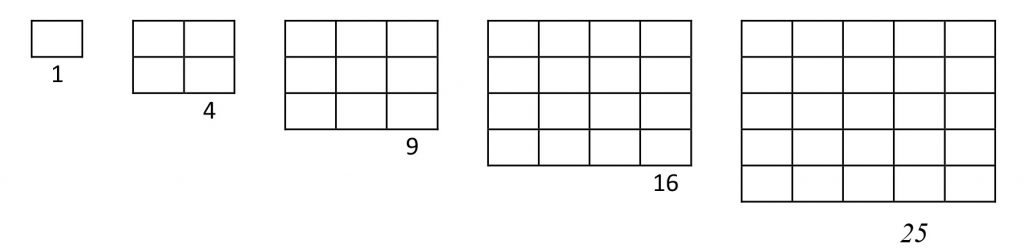
Počty kameňov v trojuholníkoch tvoria postupnosť 1, 4, 9, 16, 25, 36, 49, 64, 71 atď. Striedajú sa v nej nepárne a nepárne čísla. Prečo?
Parita v prírode
Parita má mnohoraké uplatnenie. Súvisí s orgánmi ľudského tela (dve oči, dve nohy, dve obličky a podobne) aj s Noemovou archou – veď z každého druhu zvierat bol na palube pár. Zaujímavou otázkou je, či boli v pároch na arche aj sladkovodné ryby a živočíchy, pretože v morskej vode by neprežili.
Ďalším zaujímavým prípadom parity sú názvy zvierat. Kým medveď a medvedica, srnec a srna, káčer a kačka sú (viac-menej) paritné, mnohé nie sú: napríklad jeleň a laň, krava a býk, baran a ovca, kohút a sliepka, hus a gunár. V rámci preskúšania týchto vedomostí sa možno spýtať, prečo niektoré druhy zvierat nemajú názvy pre obidva rody – a navrhnúť žiakom, aby alternatívy vymysleli. Mohli by ich doplniť do nasledujúcej tabuľky:
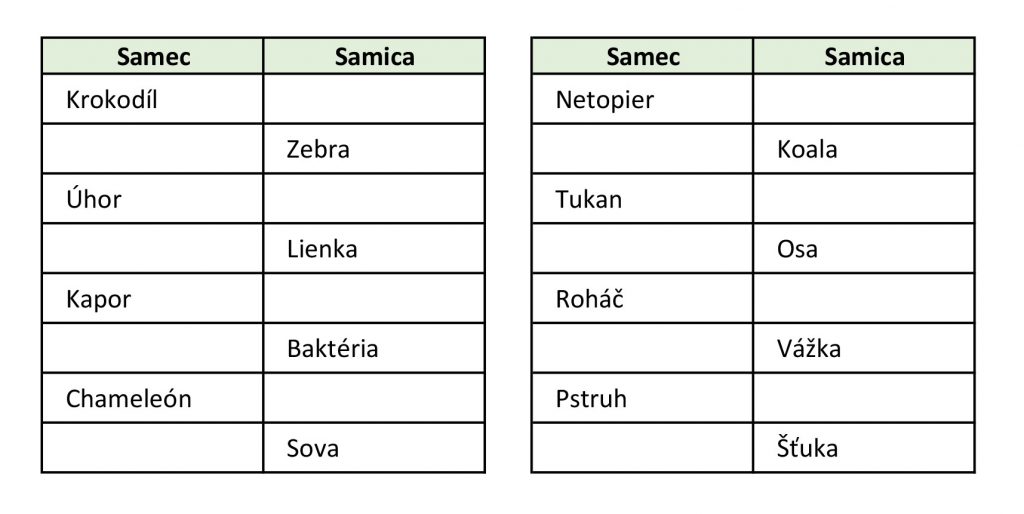
Nájdete aj iné situácie, v ktorých je parita, resp. jej absencia, nástrojom rozvoja poznatkov?

