Nielen názov tohto článku znie absurdne – také sú aj zadania v ňom
Inšpiráciou mi bol článok Does the huamn mnid raed wrods as a wlohe? – Vmína ľusdká myesľ slvoá ako ceolk? Psychológovia Grainger and Whitheyová v ňom ukázali, že zámena vnútorných písmen v slovách nebráni správnemu čítaniu a interpretácii. Protiklad medzi zrozumiteľnosťou obsahu a vysokým počtom chýb naznačuje, že drobné nedostatky vo vedomostiach nemusia byť prekážkou správneho pochopenia celku. Žiaľ, strach pred nekompletnosťou všetkých detailov neraz vedie učiteľov k preplneniu učebnej látky na úkor prezentovania celku. Takýto prístup ignoruje skutočnosť, že práve rozsah a množstvo môžu zastrieť primárny obsah posolstva.
Cieľavedomé „nezmysly“ obsahujúce náznak riešenia alebo cesty k nemu, dovoľujú rozvíjať vedomosti bez toho, aby žiaci dostali hotové riešenie. Nejde teda o nezmysly vo význame „hlúposť“. Ide skôr o absurdity s netradičnou vnútornou logikou. Ich nezriedka interdisciplinárny charakter umožňuje uplatniť kreativitu učiacich sa a tým rozvíjať tacitné (podvedomé) vedomosti žiakov. Viužlyi ste nčieo pobodné na sjevoj hidone?
Permutácie vnútorných písmen a slovenčina
Názov článku Graingera a Whitneyovej je zrozumiteľný pre pokročilého znalca angličtiny, kým pre menej zdatných je bezobsažný v obidvoch verziách – použitej aj gramaticky správnej. Potvrdzuje tým, že bez určitého penza vedomostí nie je porozumenie čomukoľvek možné a dosvedčuje starú múdrosť: Múdremu napovedz, hlúpeho trkni.
V úvode môžeme žiakov motivovať textom, ktorý má požadovanú vlastnosť. Prvé a posledné písmeno sú na svojom mieste, ale vnútorné sú permutované: Pteer a Odrnej sú dvjičoky. Ľduia si ich čtaso mýila. Chplcai to očabs znežíuavjú, havlne v škloe.
Text sa dá využiť napríklad vo výučbe materinského jazyka. Ozrejmuje, prečo gramatické chyby nemusia zničiť zrozumiteľnosť napísaného. Zároveň môže byť úvodom do diskusie, či treba mať štandardizovanú podobu jazyka vyjadrenú sústavou presne definovaných pravidiel (slovenského) pravopisu. Žiaci často namietajú, že presná gramatika nie je dôležitá. Ako ukážeme v ďalšej časti, matematika môže poslúžiť ako protiargument. S dĺžkou slova totiž počet „čitateľných“ permutácií prudko rastie, napríklad osempísmenové slovo neohybný ich má 720, medzi nimi aj nnhybeoý či nybonehý. Keby začal každý používať vlastnú formu zápisu, nerešpektujúcu ostatných používateľov, skončilo by to absolútnym chaosom. Modifikovaný text sa dá totiž čítať vďaka tomu, že myseľ transformuje chybne zapísaný text na štandardizovaný. Neexistencia štandardu je vážnou prekážkou porozumenia – je nevyhnutný a každý by ho mal poznať.
Permutácie vnútorných písmen a medzipredmetové vzťahy
Prvou „matematickou“ otázkou je: Ktoré slová sa nedajú takto zmeniť?
Nielen jedno a dvojpísmenové, ale aj trojpísmenové – jediné vnútorné písmeno nie je s čím zamieňať. Tento poznatok sa môže zdať nepodstatný, je však dôvod ho zdôrazniť. Učiteľ matematiky už teraz vie, že počet všetkých „zrozumiteľných“ zámen je faktoriál počtu vnútorných písmen. Predchádzajúca otázka je článkom propedeutiky faktoriálu – čiastkový poznatok, že „faktoriál jednej má hodnotu jeden“. Pripravil som dlhší text na tému Hŕŕ do hôr! Tu je jeho ukážka:
Ján má rád Aňu, Aňa to vie. Sú pár: Ján je Lev, Aňa je Rak.
Ján ju zve: Aňa, je jún a ide nov. Poď na pár dní do hôr!
Aňa: Kam?
Ján: Mám tip – hor sa na Choč a na Hrb. Na tri dni.
Aňa: Les nie je Rím ani bál. Len ker, tŕň, tis, buk a dub, sem-tam dym. Je tam aj vlk, had, výr, či myš, osy a iný hyd.
Ján: Boč od nich. Veď je tam aj jež, hýľ, plch, krt a páv.
Aňa: Sú aj v ZOO.
Ján: ZOO nie je háj. Je to gýč. Poď cez les, sad, lán a íl.
Okrem rozširovania slovnej zásoby sa žiaci môžu dozvedieť, že texty mávajú aj „matematické“ zákonitosti.
Permutácie vnútorných písmen a matematika
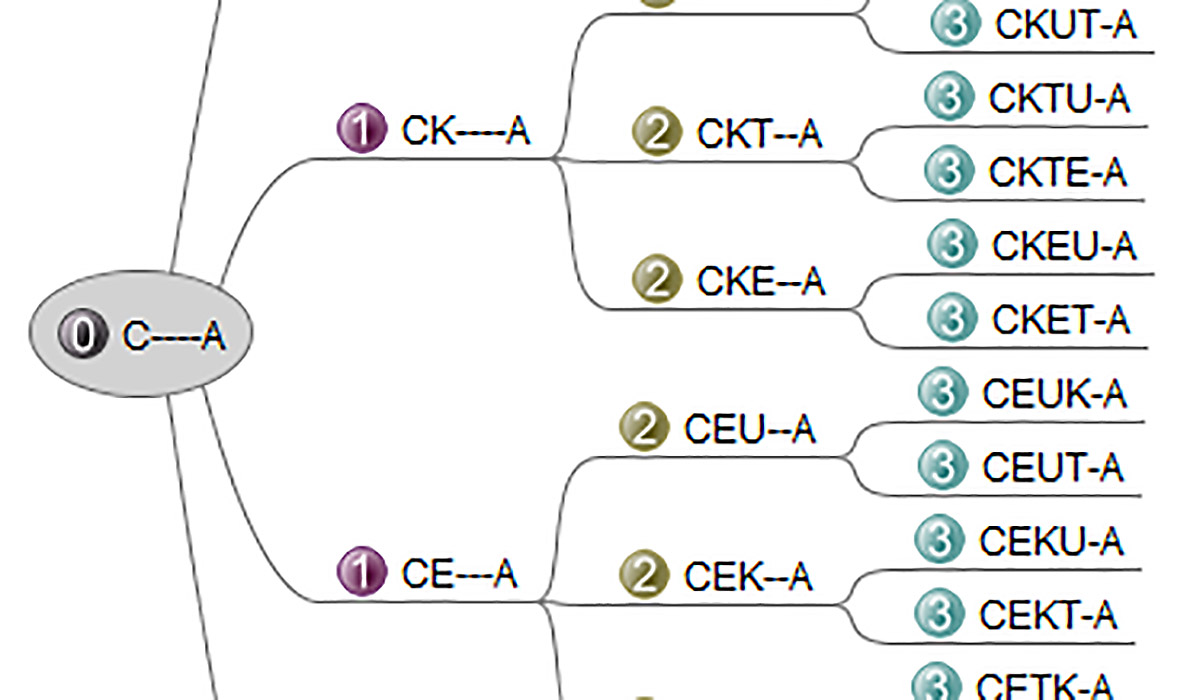
Ak je N počet vnútorných písmen N, počet permutácií bude N! iba vtedy, keď sú všetky rôzne. Na začiatku treba preto voliť krátke slová, v ktorých to platí. Kreslením vetvení na základe zostávajúcich (zatiaľ nevložených) písmen žiaci ľahko zistia, že počet vetvení sa na každej úrovní mení. Ako príklad uvádzame alternatívy slova CUKETA. Začíname „slovom“ C—-A. Prvé a posledné písmeno sú na svojom mieste, medzi nimi sú štyri medzery pre vnútorné písmená. Umožňujú štyri alternatívy, zodpovedajúce vloženiu písmen U, K, E a T: CU—A, CK—A, CE—A, CT—A.
Doplnenie jedeného z troch zvyšných (zatiaľ absentujúcich) písmen do každého z predchádzajúcich štyroch slov vedie k dvanástim nedokončeným permutáciám:
CU—A: CUK–A, CUE–A, CUT–A
CK—A: CKU–A, CKT–A, CKT–A
CE—A: CEU–A, CEK–A, CET–A
CT—A: CTU–A, CTK–A, CTE
Ešte stále existuje možnosť voľby, pretože pri každom z dvanástich neúplných slov si vyberáme z dvoch voľných vnútorných písmen.
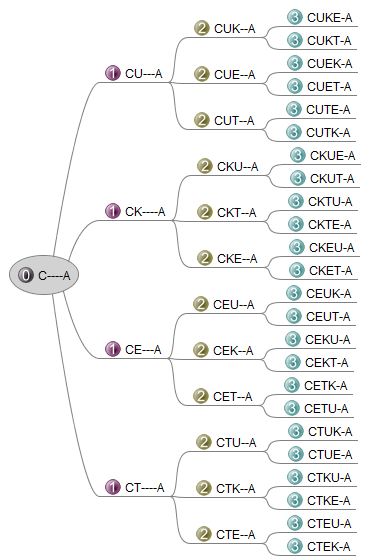
Je čas prerušiť generovanie permutácií a začať klásť otázky:
Vetvení je dvadsaťštyri. Zväčší sa ich počet v nasledujúcom kroku?
Ktoré iné slovo sa vetví rovnakým spôsobom?
Ovplyvní opakovanie vnútorného písmena (napr. v slove perleť) počet „zrozumiteľných podôb“ slova? Ako?
Ovplyvní zhoda niektorého vnútorného a vonkajšieho písmena (napr. v slove mramor) počet permutácií?
Od žiakov treba zároveň žiadať vysvetlenie ich názoru – prečo ich tvrdenie platí, resp. prečo neplatí tvrdenie opačné. Učiteľ sa môže pýtať, či je isté, že týmto spôsobom vygenerujeme všetky možné permutácie vnútorných písmen – a ako to dokázať.
Výhodou úloh je možnosť využiť bežné poznatky žiakov. Napríklad počet vetvení v slove cuketa sa postupne redukuje zo štyroch na tri, potom na dve až po jedno. Posledná možnosť môže byť pritom predmetom diskusie, či aj „jedno vetvenie je vetvenie“. Aby boli slová úplné, musíme spraviť ešte jeden krok k slovám úrovne 4, lebo iba ony obsahujú všetky vnútorné písmená. Tento prístup ozrejmí, prečo N! = N x (N-1) x … x 4 x 3 x 2 x 1.
Pomocou úloh, v ktorých permutujeme opakujúce sa vnútorné písmená, dokážu žiaci usúdiť, že každé opakovanie zmenší pôvodný výsledok K! – krát, kde K je počet jeho opakovaní daného písmena. Hoci nejde o nijako prekvapujúci a z hľadiska matematiky ani významný poznatok, ak naň učiaci sa príde sám, môže hrať dôležitú úlohu pri budovaní jeho sebadôvery.
Permutácie vnútorných písmen a informatika
Ochrana osobných údajov a komunikácia prostredníctvom sociálnych sietí patria k najdiskutovanejším témam súčasnosti. Čoraz častejšie sa preto komunikácia šifruje. Slová s permutovanými písmenami umožňujú skomplikovať dešifrovanie správy, ktorá ich obsahuje. Pri odhaľovaní kódu sa totiž veľmi často využívajú frekvenčné charakteristiky, typické pre daný jazyk (t. j. často sa vyskytujúce zhluky písmen). V slovenčine sú takými napríklad dvojice ka-, po-, vy-. Vhodnou zámenou písmen v slovách, ktoré ich obsahujú, dokážeme ich frekvenciu znížiť. Text zostane zrozumiteľný, len ho bude ťažšie dešifrovať, keďže sa skupiny hlások nebudú opakovať tak často, ako je to pre daný jazyk typické.
Myšlienka spracovať text tak, aby v ňom boli frekventované dvojice permutované, sa dá využiť ako praktické cvičenie pre vyspelejších programátorov. Úloha obsahuje rozklad slov na písmená a požiadavku vykonať zmenu poradia vnútorných písmen na základe frekvenčnej tabuľky najčastejších dvojíc a trojíc.
Medzipredmetové vzťahy nesmú byť umelé, nanútené. Musia jednak plniť úlohu v rámci samotného predmetu, jednak prirodzenou cestou odhaľovať väzby medzi zdanlivo nesúvisiacimi poznatkami. Vďaka tomu odpovedajú nielen na otázku čo, ale aj prečo. Ak sa to podarí, žiakov pocit heuréka je o to výraznejší.